Just Intonation compared to Pythagorean Tuning and Equal temprament

There have been many different tuning methods throughout time and none of them are perfect for all music. This is because music is based on intervals between notes, and those intervals do not always add up when yous switch key.

According to Ptolemy's intense diatonic scale, which is considered the only tuning that could be reasonably sung, and corresponding with modern just intonation. Gandharva Veda uses this system of tuning which means that the resonance between all the different notes will be preserved. The C major scale looks like this if we use 528 Hz as the starting note.

C = 528 Hz
D = 594 Hz (528 x 9 / 8)
E = 660 Hz (528 x 5 / 4)
F = 704 Hz (528 x 4 / 3)
G = 792 Hz (528 x 3 / 2)
A = 880 Hz (528 x 5 / 3)
B = 990 Hz (528 x 15 / 8)
Next octave of C = 1056 Hz (528 x 2)

All of these frequencies interact harmoniously with each other and all intervals are perfect equations with small . It also works with A minor, since that scale uses the same notes. However, if someone played a C major song and switched to D major, A would be the fifth and should equal 594 Hz x 3 / 2 = 891 Hz, which is quite different from the A = 880 Hz in C major. Your ear can hear difference a difference of 1 Hz between two notes that are sustained, so 11 Hz is a large difference.

Pythagorean tuning is not even harmonious within a single key and uses only perfect fifths (3:2) and octaves (2:1) which creates very large integers, such as 243:128 for a major seventh which comes from five fifths up and two octaves down (3/2)5 x (1/2)2. The big downside is that thirds (which form the middle note in chords) are dissonant - they are 81:64 instead of 5:4, which means for the above example E = 668.25 Hz instead of 660 Hz. Those extra 8.25 Hz means that musicians working with Pythagorean tuning can't play regular chords, but have to stick to simpler music using mainly fifths instead.

With Equal Temperament musicians figured out a way to play all different keys on the same instrument with a harmonic sound. Even though Equal Temperament is often viewed as a Western invention, it has been historically discovered by a Chinese man in 1584 and a Dutch man in 1585, independent of each other. Instead of working with intervals that relate to each other in mathematical harmony, equal temperament simply divides the octave into 12 equal pieces.

The downside of Equal Temperament is that some tones are more than 4 Hz higher or lower than their Just counterparts, which is a clear audible difference. This means that a perfect fifth, which is 3:2 in Just Intonation, will instead be 2.996614:2 in Equal Temperament. In Just Intonation the fifth and the unison would resonate with each other every 2 beats for the fifth and 3 beats for the unison. However, in Equal Temperament the fifth will slowly go out of beat with the unison since there is no exact mathematical relationship.

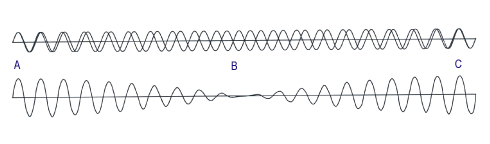
This means that instead tones strengthening each other, they destructively interfere with each other, as can be seen in the following image from a lecture held at Maharishi Vedic University, Vlodrop, Holland, in January 2011.

"The two upper waves are the sounds, while the wave under is the combined sound that we hear. The two sounds have the same amplitude. The changing amplitude of the lower wave shows the change in volume of the combined sound. At point A the two sounds are somewhat synchronous, and the combined amplitude is at its largest. Then they become less synchronous and the combined amplitude becomes less. At B they vibrate opposite each other and the combined amplitude becomes zero, making no sound. Then they gradually move back to synchrony, while the combined amplitude gradually increases and reaches its maximum when the two waves again become synchronous, and so on."

So, even if you have tuned your guitar to A = 432 Hz, the guitar itself does not use Just Intonation and so even if A is the right frequency, no other tones will be. The easiest way is to play a fretless instrument, such as the violin, since you can adjust each note as you please. However, with guitar and keyboard there are no easy solutions to this, unless you want to build your own guitar like this guy did!